We use Elastic-Plastic Self-Consistent (EPSC) modeling to interpret the diffraction data collected with the D-DIA apparatus. In particular we the EPSC Model of Turner and Tome (1994). Elastic-plastic self-consistent (EPSC) models consider the elastic and plastic behavior of a polycrystal by examining the behavior of large numbers of individual grains. Each grain is treated as an elliptical inclusion within an infinite homogeneous matrix, which in turn, has the average properties of all of the grains in the polycrystal. Each grain is described by its orientations, its single crystal elastic tensor and possible slip systems, each with its own critical resolved shear stress (CRSS).


Figure 1. Principles of elastic plastic self consistent models utilizing Voce hardening law.
An increment of strain is applied to the homogenous matrix that transmits stress to the grain. The grain responds elastically or plastically depending on its orientation and the CRSS of its slip systems, while also fulfilling compatibility criteria. The behavior of the homogenous matrix is the sum of the behaviors of the remainder of the grains and must be recalculated after each grain is deformed. Thus the model iterates until it converges for each deformation step. Work hardening may also be included in the model.
Model output includes stresses and strains for each grain as well as average stress and elastic strains for populations of grains that contribute to various diffraction peaks. The macroscopic stress and strain for the aggregate are also calculated. Therefore, model results can be directly compared with diffraction results.
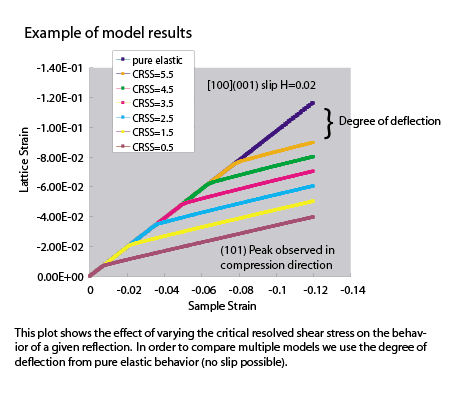
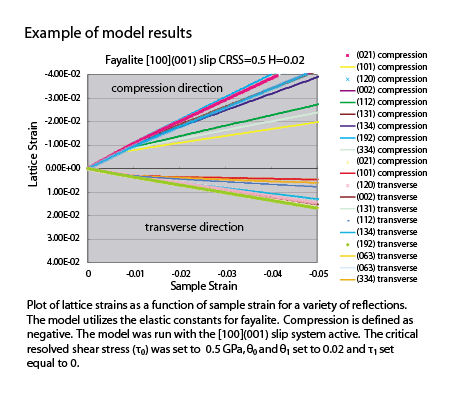
Figure 2. Example models for fayalite olivine